Wait Determination

Determining your wait amongst a large number of tiles in the same suit is one of the most difficult and time-consuming parts of the exam. It requires you to quickly look at the same tiles in the same hand in a number of different ways.

While these information here is effective overall, it will include elements that do not work at a mahjong table. This guide is specifically to increase your ability to pass the written exam, and will take into account the method the question is given, and the time and resources available to you.

Practice

Regardless of which methods you use, here is an app to generate and practice wait determination on.

Priorities

First, and most important, is getting the correct answer. This means not only picking out all of the waits available, it means successfully not picking any other tiles as waits. After you are able to do that, you can either get faster at the method you are using, or add or switch to a different method. Tiles revealed as “waits” or “not waits” by one method do not need to be checked again by other methods. So, if you know a number of methods at different competency and speed levels, you can mix and match. We will go over a number of methods below, after some fundamentals.

Fundamentals: No Isolated Tiles

An important, if possibly obvious, thing to remember is that every tile in the hand is either part of a pair, sequence, or set. If you can’t use it in one of these three things, it is not a complete hand. This means you can narrow down the range of possible tiles that complete a hand. An example:
etc.
the first 1 is eventually either part of a pair or a sequence. and that sequence has to be 123. however:
if you use existing tiles, or add a 4 or higher, that leaves an isolated 2 (123 2 34xxx)
if you add a 1, you either have a hanging 12, or a 2 (with 11 2 234).
So, regardless of the rest of the hand’s makeup,
this hand cannot be waiting on 1, or 4-9.

When “testing” if a certain tile is a wait, add the tile, and then start with either end of the hand, and ask the following for each tile until either you use them all (it’s a wait) or there is no way to use them without having an isolated tile:

• it is part of a triplet
• is it part of a pair (and you don’t have another pair already)
• is it part of a sequence

We will do an exhaustive example. To see it (it is quite lengthy), click the tab below. Afterwards, look below it for ways to do this a lot, lot faster.

Exhaustive Waitfinding Example: 2344445556667 (Click/tap for full example)

Yikes. Shortcuts below.

Fundamentals: Wait Shapes

As a hand is four sets/sequences and a pair, seven different pairs, or thirteen orphans (one paired), and being tenpai is one tile less than that, you learn through playing the basic waits to finish a hand. for example,
>
>
>
and so on. Other common ones that come up are shapes like
>
>
>
>
As you play, these more common ones stop being waits that you don’t calculate, but know by rote. By memorizing them, you pick up speed in wait determination.

So, to solve larger waits, you need to increase the wait shapes you know immediately.
Start with “one set/sequence and a pair” (4-tile), and add one set/sequence at a time.
Your intermediate goal should be to memorize these 3 4-tile waits and 18 7-tile waits. Also, please be certain to learn them “the other way” as well: 2345666 and 2223456 are the same shape, mirrored. Learn to see both.

(A quick note: I want to thank Kakkoii Mahjong Series for a breakdown of 7-tile shapes, and the removal/replacement method. You can find their videos and writings online, as well as a store with their mahjong-inspired clothing line. Great stuffs!)

4 tiles:
>
>
>

7 tiles:
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>

Fundamentals: Connected Waits

When you find a wait, there is a good chance you automatically found another, connected, one. Of course, if a hand already has 4 of the connected tile, that wait doesn’t count. This will shortcut you past testing certain waits, saving you valuable time.

Connected Wait Type 1: If the tile you added is “off the end” (lower than all tiles / higher than all tiles) of your wait shape, the suji is a wait as well, as your wait is automatically part of a double-sided wait. Examples: in 2344777888999, when you check for the 1 wait, and find that it works, as the 1 is “off the end” of it. this means the 4 is a wait. For 1112223336678, the 9 working means the 6 does as well.

Connected Wait Type 2: If the tile you added is part of a triplet, your pair is a wait as well, as your wait was a double-pair wait. Examples: with 1144556677799, testing a 1 works (111 456 456 777 99), so then a 9 works as well.

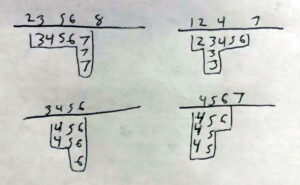
Preferred Method for the Exam: Dropdown

This on-paper method was developed for the Rochester clubs by myself, attempting to find a way to run through all the waits for confirmation in the approximate 55 seconds you are given per answer. It requires a bit of pen and paper, and is much more effective if you have good penmanship and spacing, as the grid-like nature of it makes it much easier to use.

If the alignment doesn’t work for you, you can try writing left to right: row of 1, then row of 2 below, etc. A number of people have found this easier with their reading / writing style.

Example:

The layout is 9 imaginary columns, the top entry of each is kept apart by a header line.

Then, each tile is written in the bottom part, multiple ones stacking up below that line. For the hand above, this is what it would look like. (numbers not written are shown as partially visible to help with visualization of where things should go)

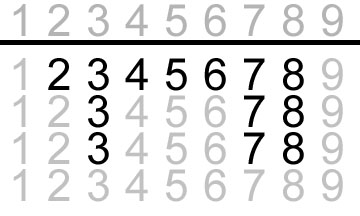
then, you either cross out / mark pairs and sets until you see a shape you recognize, or pick a tile from above the line and “test” it in the picture. For example, this is a successful test of 1:

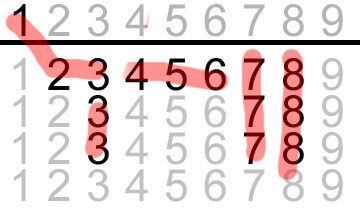
that 123 used as such means 4 also works:

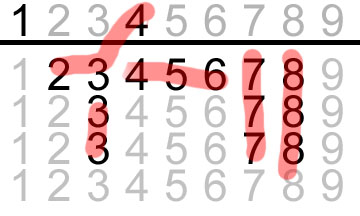
2 works as a pair wait:

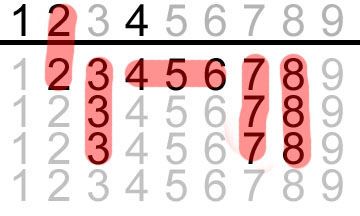
3 works as a 2_4 wait (or a double pair of 3 and 7, try it yourself):

and 7 works with the 56.

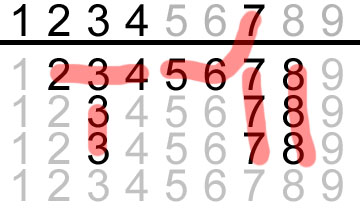
For here, you can test each other wait quickly, and see that it doesn’t fit (in that the hanging 2 means you are locked into a 33 pair, 234 and 567 sets)

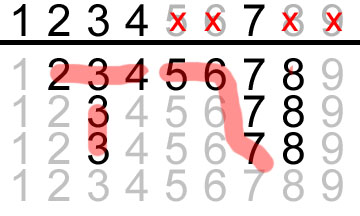
So your waits for this hands are 12347.

You can replicate this on paper. Now, crossing things off can get messy, so I suggest first pass “circling”, second pass “light line”, third pass “heavy line”, so you don’t have to take time rewriting and can still see the numbers under them:

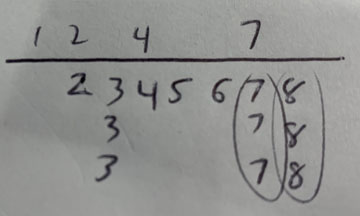
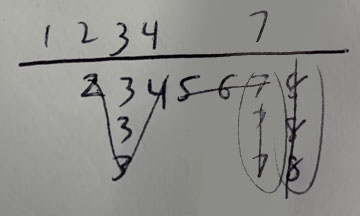
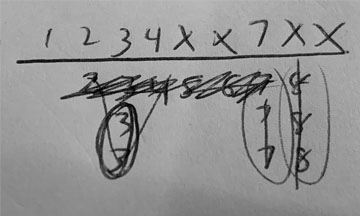
You can also “cut” from the sides with your pen as a physical block to look for shapes to pre-fill in numbers. Finding early shapes is essential for speed, as this can “knock out” two to four waits quickly, as well as let you know where you can stop looking (for example, with the above hand, once you’ve checked 1234 you know that 234 is a sequence and 33 is your pair. After you check 5, you know that 567 is another sequence). Below’s example shows , which is 1247:

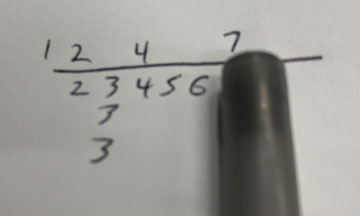
Work on recognizing waits and cutting down time with the methods above to get your wait determination time under a minute to help with your exam preparations.

Tip! Increasing Speed with Dropdown: Add the Fundamentals of Connected Waits and Tile Shapes to your work. For Connected Waits, if the problem has 2 as the lowest tile, and a 1 works, then unless you have all the 4 already, the 4 works as well. For Wait Shapes, as you write the problem down, if you can quickly cover two mentsu and look at the remaining 7 tiles, if that is a wait shape you know, fill them in immediately. You’ll learn to see these things graphically as you practice this: 4455666 is three buildings together (a 2-story, another 2-story, a 3-story). 4555666 is the same (a 1-story garage, then a 3-story and another 3-story). Every wait you knock out this way is 5-10 seconds bonus, which adds up very quickly.

Tip! Increasing Speed with 7-Tile Waits: When you are processing a full flush, standalone edge tiles, once the tiles “before” them and “like” them are tested, that tile will only be usable in a sequence where it is the edge tile. Since, for a successful wait, all tiles must be used, and this is the only way this tile can be used, you remove that sequence completely from the problem. If you do this twice, you are left with a 7-tile wait and can find the remaining answers immediately.
Example: . 

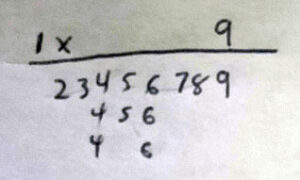
From the left, after testing 1 (which works: 123 444 55 666 789) and 2 (which doesn’t: 22 345 456, hanging 4), you will now only be testing 3 through 9. This means that standalone 2 in the hand can only be a part of the already existing 234.

From the right, after testing 9 (which works: 234 456 456 678 99), you will now only be testing numbers below 9. This means that the standalone 2 in the hand can only be part of the already existing 789.

Since those tiles are locked, remove them.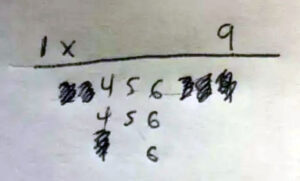

having removed the 234 and the 789, you are left with 4455666 – which is a 7-tile wait, outputting 3456. The waits for this flush are 134569. If you familiarize yourself with what the 7 tiles waits looks like as shapes, they will become more recognizable:

Alternate Method: Removal and Replacement

Please note: the Preferred Method was what was used on the actual exam successfully. However, if you would prefer another method that was used by players how passed, this may be an option.

What Removal means is to take tiles away from a series of tiles, one set/sequence/pair at a time, until the remaining is a formation you recognize. Making a note of those waits, you then remove tiles in a different manner, seeing if other waits appear. Since, as above, all tiles are used in a sequence, set, or pair, once you’ve checked all possible ways to use the tiles, you have your list.

For example from above:

Taking the 123 out leaves 4666, which is a 45 wait.
Taking the 666 out leaves 1234, which is a 14 wait.
(Taking the 66 out leaves 12346, which is also a 5 wait)
So the waits are .

Replacement means to remove tiles until you have a wait sequence, then look at what was removed, put back one of the tiles that finishes the final wait, and seeing if that then makes a wait of its own. This can quickly add correct waits to your list without having to hunt down more variation.

For examples:

Taking out the 567, you are left with 3335, which is a 45 wait. One of those tiles, the 5, you already “took out”. So if you put it back, your taken out tiles are now 67, which is a 58 wait. Total wait is .

If you have a triplet, taking it out, and then returning one tile, can be very helpful.

removing the 888 you get 1234567, which is a 147 wait. Adding back an 8 you get 12345678, which is 123 45678, a 369 wait, totaling .

If you take a sequence out, and then one side of that sequence fills the wait, then the other side of that sequence is also a wait.

Removing 234 leaves 4556688, which can be filled with 4 or 7. since the 4 can come from the end of 234, then 1 is also a wait, as that leaves a 23. Combining the waits gives you .